ICE-BA论文学习
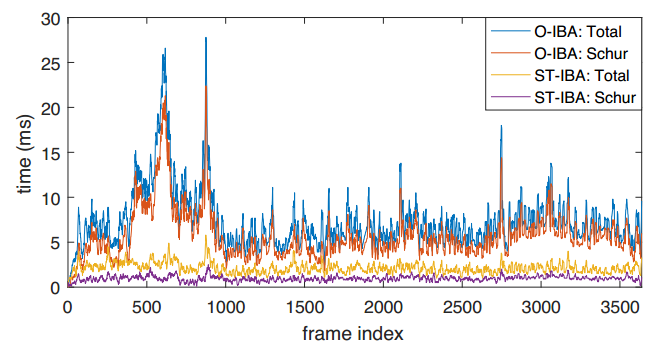
在Bundle Ajustment的线性方程组中,通常采用Schur消元法进行求解,而Schur消元这一操作占用了迭代中的大部分时间,如下图所示。ICE-BA对H矩阵采取增量更新的方式加快了BA优化的速度,从而使得滑动窗口中可以包含更多的帧数来联合优化,提高SLAM性能。
增量式BA
前面提到在BA中,Schur消元占用了主要的时间。两帧$i,j$之间的共视点会对两帧的位姿产生约束,使得海森矩阵H中相应的块$S_{ij}$非零。在执行Schur消元时,是可以分块进行的,通过一个共视约束,更新相应的块$S_{ij}$以及方程右边的残差量。
文献1中提出的RKD-SLAM中,采用了增量式BA的方法(incremental BA),其核心思想是,每次迭代时不用对所有点均进行Schur消元。在SLAM的滑动窗口中,优化变量是随着新的关键帧不断增加的,而之前已经优化过的变量在优化中变化很小,对于那些变量,每次Schur消元的变化是很小的。因此,在增量式BA中,点的线性化和Schur消元只发生于两种情况:
- 产生了新的观测
- 点的更新量大于某个阈值
如此一来,考虑到同一个点在不同滑动窗口中的稀疏共视关系,每次迭代需要线性化和Schur消元的点数量就能减少,提高了计算效率。相应地,这样做应该会增加存储空间,因为需要保存每个共视约束上一次对海森矩阵块的贡献。
ST-IBA
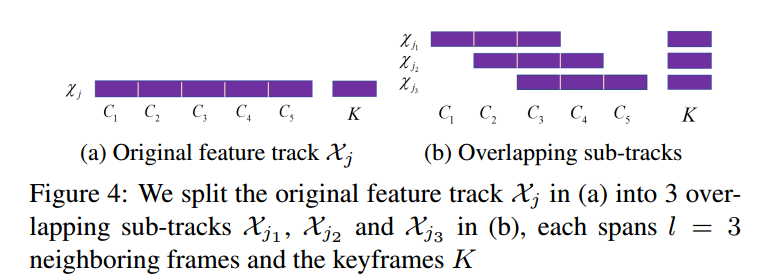
在ICE-BA2中,包括Local BA和Global BA,在LBA中,由于每个点的共视帧太多,导致每当产生新的观测时,在Schur消元中需要重新线性化的残差项太多。因此,ICE-BA提出了Sub-Track方法,将一个包含多个帧的关键点跟踪划分为几个重叠的小段跟踪,如下图所示。
Sub-Track说的简单一点其实就是把原来没有稀疏性的矩阵变成一个带状的稀疏矩阵。上图中的划分中,将一个跟踪划分成了三段,这三段跟踪的是同一个3D点。原本相机$C_1,C_4;C_1,C_5;C_2,C_5$之间是有约束的,经过分段划分后去掉了这些约束,矩阵块$S_{14},S_{15},S_{25}$都为0,原来的海森矩阵H变为一个带状矩阵,为其增加了稀疏性。另外,当产生新的观测时,由于共视帧更少,需要线性化的残差项也减少了。
ICE-BA中将Sub-Track的长度取为$l=5$。需要注意的是,Sub-Track只影响Schur消元以及线性化的残差个数,后续点的状态更新与Sub-Track并没有关系。
增量式PCG
ICE-BA中对PCG进行了一个改进,就是其迭代初值的选取。由于PCG是一种迭代求解线性方程组的方法,如果有一个比较好的初值有利于PCG的收敛。在ICE-BA中这种增量式BA中,并不是所有变量都会进行更新,只有当$\delta x$大于门限时才会更新,如果一个变量本次没有更新,其实下一次计算出的$\delta x$也不会差太多,因此可以将PCG中的初值置为上一次的结果,加快收敛速度。
相对边缘化
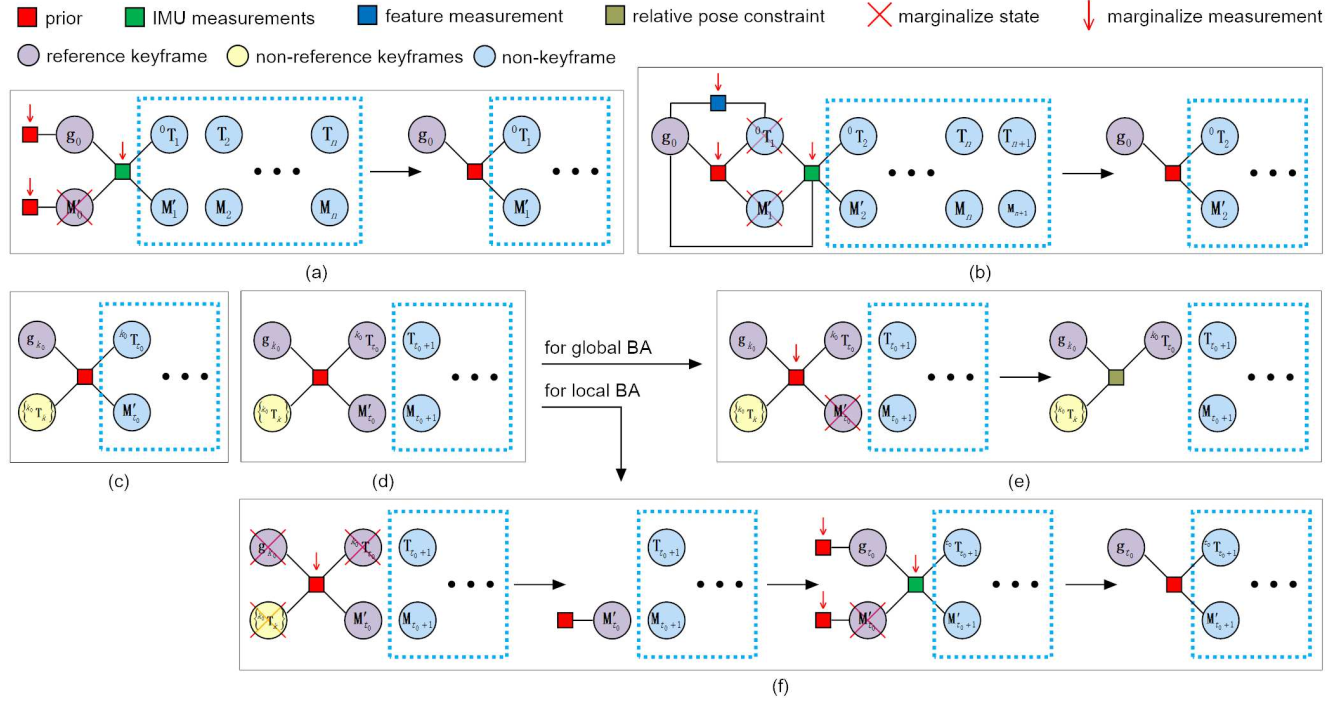
ICE-BA中的关键帧在Global BA中优化,Local BA中优化最近的50帧。由于误差的积累,边缘化产生的prior会越来越不准确,如果加入到Global BA中进行优化,会降低精度。为了保证Local BA中边缘化的约束在Global BA中能够保持一致性,边缘化时采用了相对位姿,边缘化约束两关键帧的相对位姿而非绝对位姿。ICE-BA中的边缘化如下图所示。
上图中的$M$表示速度和IMU偏置,可见其只在Local BA中进行优化,在Global BA中对$M$直接边缘化,保留其他优化量。